Deformation Caused by Filling of a Caisson (FLAC2D)

Problem Statement

Note

This project reproduces Example 2.5.5 from FLAC 8.1. The project file for this example is available to be viewed/run in FLAC2D.[1]. The project’s main data files are shown at the end of this example.

This academic example studies the mechanical deformation caused by infiltration of water in a caisson filled with a porous material. The caisson is 6 m in width and 6 m in height. Initially, the bottom 2 m of the caisson is fully water saturated and steady-state conditions prevail. The top of the caisson is then exposed to a constant flux of water (flow rate of \(q=0.2\) m/day) on a span of 1 m located at the center. During the experiment, the water level is kept at the initial height on the later sides. The evolution of saturation and soil deformation is monitored for a total of 20 days. The fluid and rock properties are given in Table 1 and 2, respectively.

Table 1: Fluid properties

Property	Value
Porosity	0.3
Sat. mobility coefficient	1 \(\times\) 10-10 m2/Pa s
Wetting-phase compressibility	0.001 kPa-1
Residual saturation	0.0
van Genuchten \(m\)	0.336
van Genuchten \(n\)	1.506
van Genuchten \(p_{ref}\)	7 kPa
Rel. permeability exponent \(b\)	0.5

Table 2: Rock properties

Property	Value
Constitutive model	elastic
Solid density	1500 kg/m3
Bulk modulus	100 kPa
Shear modulus	30 kPa

By symmetry, half of the caisson is considered in the numerical model. The left vertical boundary is the symmetry line. The modeling domain is discretized by 12 zones in the horizontal direction and 24 zones in the vertical direction. The mechanical boundary conditions correspond to zero normal displacement at the lateral and bottom sides of the caisson. Lateral displacements are also restricted at the bottom of the model, i.e., fixed in both directions. Moreover, the relative permeability of the wetting-phase is given by:

(1)\[k_{rw} = S_{w}^{b} \left[ 1 - \left( 1 - S_{w}^{1/m}\right)^{m} \right]^{2}\]

where \(k_{rw}\) is the relative permeability of the wetting-phase, \(S_{w}\) is the water saturation, \(b\) is the relative permeability exponent, and \(m\) is a van Genuchten fitting parameter.

Changes in wetting-phase pressure \(p_w\) are governed by the following equation, assuming isothermal conditions:

(2)\[\frac{1}{M} \Delta p_w = \frac{1}{S_w} \Delta \zeta - \frac{\phi}{S_w} \Delta S_w - \Delta \epsilon \quad \mathrm{or, equivalently}\]

(3)\[\left(\frac{1}{M} - \frac{\phi}{S_w} \frac{\Delta S_w}{\Delta p_c}\right) \Delta p_w = \frac{1}{S_w} \Delta \zeta - \Delta \epsilon\]

where \(M\) is the saturated Biot modulus, \(\zeta\) is the variation of fluid content, \(\phi\) is the porosity, \(\epsilon\) is the volumetric strain, and \(p_c=-p_w\) is the capillary pressure, or suction. The term on the left hand side of equation (3) and in brackets is the inverse of the Biot modulus in partially saturated conditions.

Initial pore pressure and saturation are are assigned using a FISH function. The distributions correspond to the steady state conditions with water level 2 m above the bottom of the caisson (\(y=2\) m). The initial stresses—in equilibrium under gravity and consistent with the initial saturation distribution—are calculated numerically during gravity initialization. The initial horizontal-to-vertical effective stress ratio is 1. The numerical model is carried out for a total of 20.8 days, with intermediate results at four additional times.

Results

Figures 1 to 4 show the saturation contours, fluid flow vectors, and deformations taking place during the filling process.

Figure 1: Deformation and saturation contours at time \(t=0\) days.

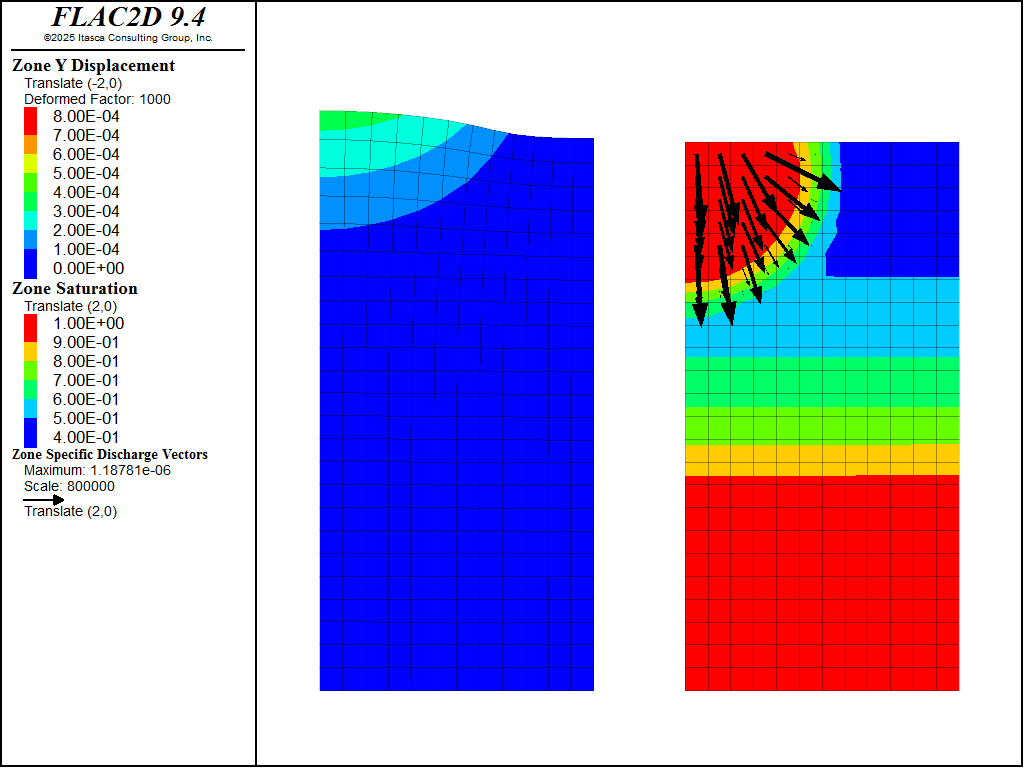
Figure 2: Deformation and saturation contours at time \(t=2.3\) days.

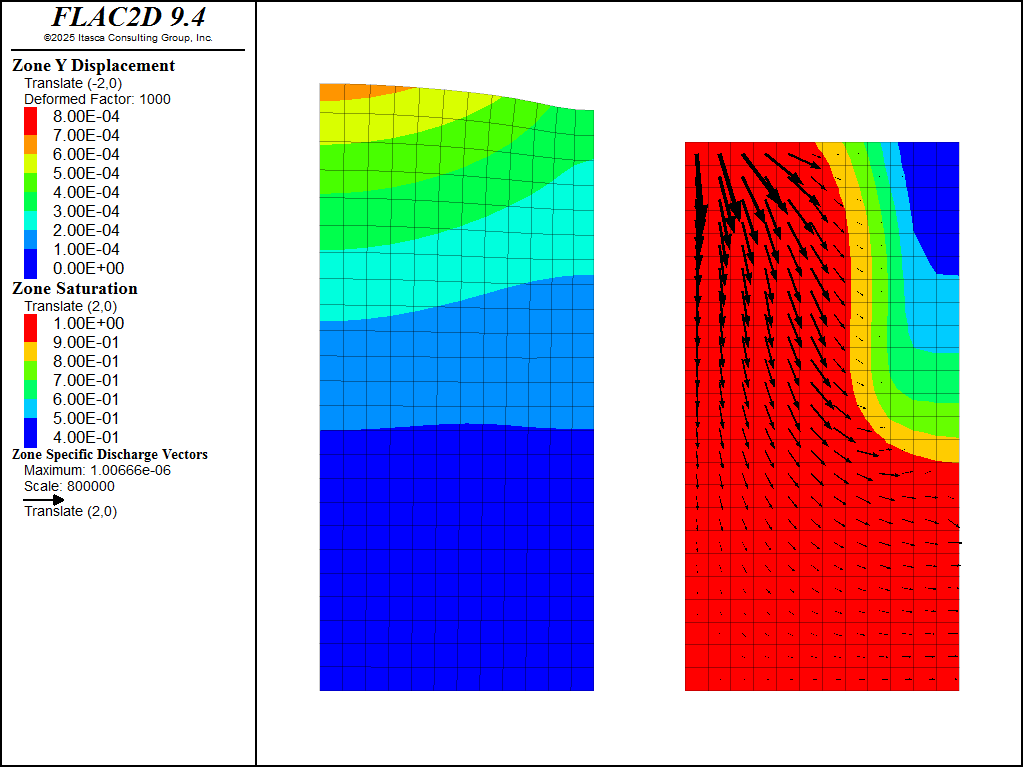
Figure 3: Deformation and saturation contours at time \(t=6.9\) days.

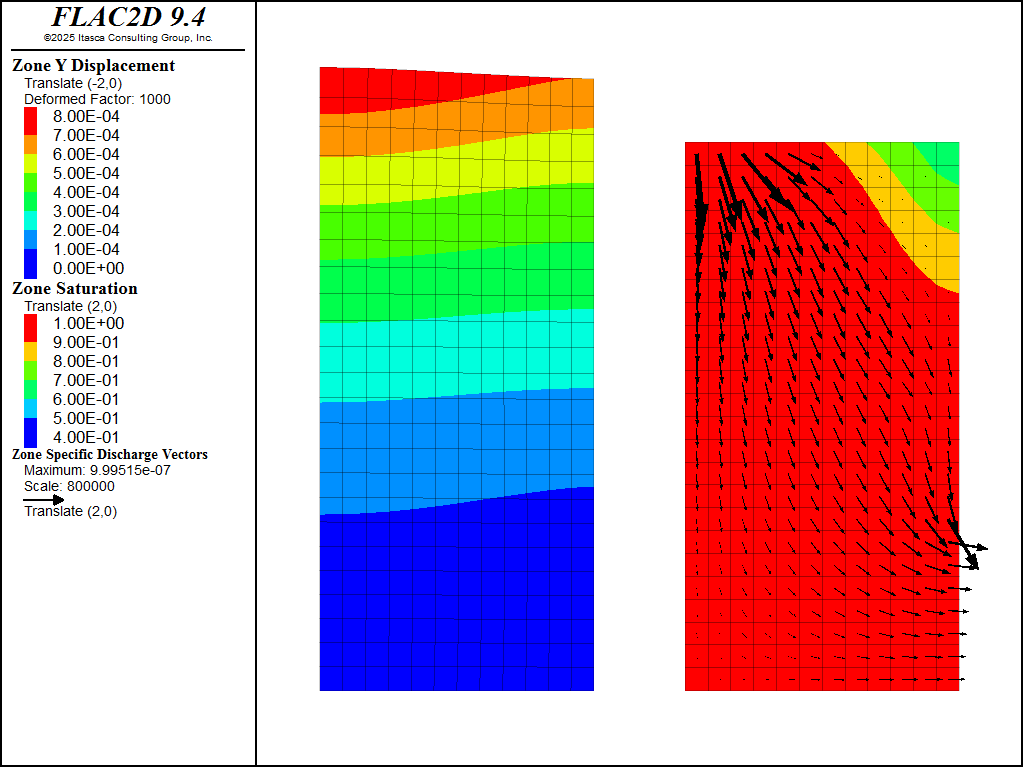
Figure 4: Deformation and saturation contours at time \(t=20.8\) days.

Data Files

filling_of_caisson.dat

model large-strain off
model configure fluid-flow
model gravity 0 -10

[Cw = 1e-6]   ; Wetting phase compressibility [1/Pa]
[Cnw = 1e-3]  ; Non-wetting phase compressibility [1/Pa]

[n = 1.506]   ; Van-Genuchten n
[m = 0.336]   ; Van-Genuchten m
[pr = 7e3]    ; Van-Genuchten pref [Pa]
[b = 0.5]     ; Relative permeability exponent

[h = 2.0]            ; Inital saturated height [m]
[q = 0.2 / 86400.0]  ; Wetting phase injection rate [m/s]

program call "functions"

zone create quadrilateral size 12 24 ...
    point 0 (0, 0) point 1 (3, 0) ...
    point 2 (0,6)
    
zone face apply velocity-normal 0 range position-y 6 not
zone face apply velocity-x 0 range position-y 0
    
zone fluid property fluid-density 1000 porosity 0.3 ...
    mobility-coefficient 1e-10 fluid-modulus [1/Cw]
zone fluid unsaturated van-genuchten [n] [m] [pr]

[init_pp]
[rel_perm]
[save(0)]

zone cmodel assign elastic
zone property density 1500 bulk 1e8 shear 0.3e8
zone initialize-stresses total ratio 1.0
model solve-static

zone fluid property pore-pressure-generation on
zone fluid property effective-cutoff -1e20
zone fluid permeability-saturation table "krw"
zone face apply discharge [q] range position-x 0 0.75 position-y 6
    
model solve-fluid-coupled time-total 2e5 convergence 2
[save(1)]
model solve-fluid-coupled time-total 6e5 convergence 2
[save(2)]
model solve-fluid-coupled time-total 18e5 convergence 2
[save(3)]

functions.dat

;------------------------------------------------------;
; Functions: Deformation Caused by Filling of a Caisson.
;------------------------------------------------------;

fish define init_pp
    ; Initialize pore pressure
    local g = math.abs(global.gravity->y)
    local gw = zone.fluid.density(::zone.list)(1) * g
    
    ; Above phreatic surface (partially saturated)
    local pos = gp.pos(::gp.list)
    local gps = gp.list(pos->y > h)
    local posa = gp.pos(::gps)
    
    local pi = (h - posa->y) * gw
    local pc = -pi
    local Swi = 1.0 / (1.0 + (pc/pr)^n)^m
    gp.pp(::gps) ::= pi
    gp.sat(::gps) ::= Swi
    
    ; Below phreatic surface (fully saturated)
    gps = gp.list(pos->y <= h)
    local posb = gp.pos(::gps)
    
    gp.sat(::gps) = 1.0
    gp.pp(::gps) ::= (h - posb->y) * gw
    
    ; Boundary condition
    gps = gp.list((pos->y <= h) and (pos->x == 3.0))
    local posbc = gp.pos(::gps)
    gp.pp.fix(::gps) ::= (h - posbc->y) * gw
end

fish define rel_perm
    ; Wetting phase relative permeability
    local tab = table.create("krw")
    loop for(local i = 0.01, i <= 1.0, i += 0.01)
        krw = i^(b)*(1.0 - (1.0 - i^(1/m))^m)^2
        table(tab, i) = krw
    endloop
end

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).