Munson-Dawson Model: Triaxial Test (FLAC3D)
Note
The project file for this example may be viewed/run in FLAC3D.[1] The main data file used is shown at the end of this example.
This verification test for the Munson-Dawson model is a typical triaxial compressive loading and unloading at a fixed temperature of 300 K (27 °C) and at a fixed cell stress (\(\sigma_{rr}\)) of 20 MPa. The procedure starts with a 20 MPa isotropic hydrostatic stress at t = 0 days. The axial stress (\(\sigma_{zz}\)) increased to 35 MPa and kept constant during the next 50 days, resulting in a 15 MPa equivalent stress over this period. Initially, the strain develops quickly but then transitions to a steady-state rate as the material experiences work hardening. At t = 50 days, the axial stress value is unloaded to 33 MPa. This 2 MPa unloading significantly slows the strain rate, which then gradually adjusts to a new steady-state rate as the material undergoes recovery over the subsequent 50 days.
The material properties are summarized in the table below.
shear
\(G\)
12.4 (GPa)
bulk
\(K\)
20.7 (GPa)
hosford
\(a\)
16
f-exponent
\(\chi\)
1
A-0
\(A_0\)
5.617e1 (\(s^{-1}\))
activation-ratio-0
\(Q_0/R\)
5123 (K)
n-0
\(n_0\)
1.595
A-1
\(A_1\)
8.386e22 (\(s^{-1}\))
activation-ratio-1
\(Q_1/R\)
12580.5 (K)
n-1
\(n_1\)
5.5
A-2
\(A_2\)
4.415e16 (\(s^{-1}\))
activation-ratio-2
\(Q_2/R\)
5123 (K)
n-2
\(n_2\)
6.279
B-1
\(B_1\)
6.086e6 (\(s^{-1}\))
B-2
\(B_2\)
3.034e-2 (\(s^{-1}\))
stress-limit
\(\sigma_0\)
20.57e6 (MPa)
stress-constant
\(q\)
5335
k-0
\(k_0\)
5.277e-2
c-0
\(c_0\)
8.882e-3 (\(K^{-1}\))
m-0
\(m_0\)
0.9201
k-1
\(k_1\)
3.052e12
c-1
\(c_1\)
8.882e-3 (\(K^{-1}\))
m-1
\(m_1\)
5.282
alpha-hardening
\(\alpha_h\)
3.367
beta-hardening
\(\beta_h\)
-0.6838
alpha-recovery
\(\alpha_h\)
0.58
beta-recovery
\(\beta_r\)
0.0
For \(\chi\) = 1, an analytical solution is available. Figure 1 plots the axial and radial strains from the FLAC3D result based on a single-zone test which is consistent to the reference analytical solution in Reedlunn (2018), both with material parameters from set I (calibration 3B of the MD model) listed in the property table. The numerical FLAC3D solution fits perfectly with the reference analytical solution. This example verifies work hardening and recovery governed by transient strain limit mechanism 1 and steady-state strain accumulation governed by mechanism 2.
References
Reedlunn, B. Enhancements to the Munson-Dawson model for rock salt (No. SAND-2018-12601). Sandia National Laboratories, Albuquerque, NM, USA (2018).
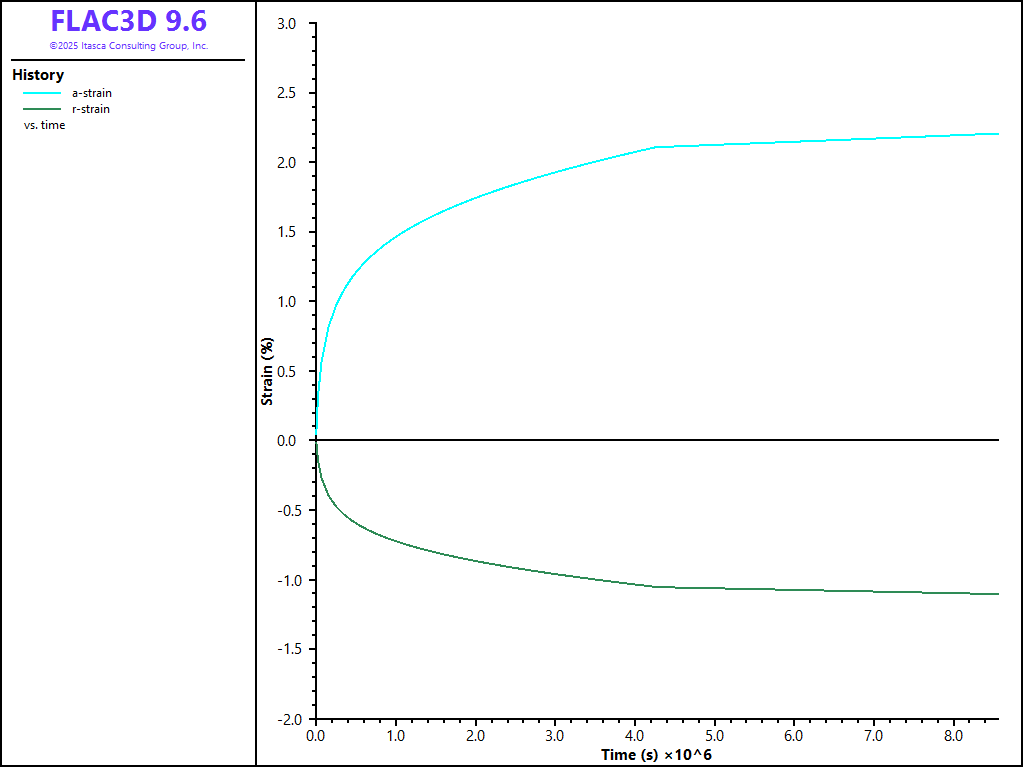
Figure 1: Triaxial test on a Munson-Dawson material: numerical strain values versus time.
Data File
model new
model large-strain off
fish automatic-create off
model title "Triaxial Compression test --- Munson-Dawson model"
model configure creep
model creep active off
;
zone create brick size 1 1 1
zone face skin
zone cmodel assign elastic
zone property density 2300 bulk 20.7e9 shear 12.4e9
;
zone initialize stress xx -20e6 yy -20e6 zz -20e6
;
zone face apply stress-normal -20e6 range group 'East' or 'West'
zone face apply stress-normal -20e6 range group 'North' or 'South'
zone face apply velocity-z 0 range group 'Bottom'
zone face apply stress-normal -20e6 range group 'Top'
;
model solve
;
model creep active on
zone cmodel assign munson-dawson
;; Cal-3B
zone property density 2300 temperature 300
zone property bulk 20.7e9 shear 12.4e9 f-exponent 1 hosford 16
zone property A-0 5.617e1 activation-ratio-0 5123 n-0 1.595
zone property A-1 8.386e22 activation-ratio-1 12580.5 n-1 5.5
zone property A-2 4.415e16 activation-ratio-2 5123 n-2 6.279
zone property B-1 6.086e6 B-2 3.034e-2
zone property stress-limit 20.57e6 stress-constant 5335
zone property k-0 5.277e-2 c-0 8.882e-3 m-0 0.9201
zone property k-1 3.052e12 c-1 8.882e-3 m-1 5.282
zone property alpha-hardening 3.367 beta-hardening -0.6838
zone property alpha-recovery 0.58 beta-recovery 0.0
; Axial-Stress to 35 MPa
zone face apply stress-normal -35e6 range group 'Top'
;
[global zp = zone.head]
[global gp = gp.find(8)]
fish define q_
global q_ = zone.stress.xx(zp) - zone.stress.zz(zp)
global a_ = math.ln(1.0-gp.disp.z(gp))*100
global r_ = 2.0*(-gp.disp.x(gp))*100
end
history interval 100
model history name 'time' creep time-total
fish history name 'dev-stress' q_
fish history name 'a-strain' a_
fish history name 'r-strain' r_
; --- creep test ---
model creep timestep starting 1e-20
model creep timestep automatic
model creep timestep minimum 1e-20
model creep timestep maximum 1000
model creep timestep upper-multiplier 0.99
model creep timestep lower-multiplier 1.01
;
model solve creep time-total [3600*24*50]
model save 'tri1'
; Axial-Stress to 33 MPa
zone face apply stress-normal -33e6 range group 'Top'
model solve creep time-total [3600*24*100]
;
history export 'time' 'dev-stress' 'a-strain' 'r-strain' ...
file "triaxial-md.txt" truncate
model save 'triaxial-md'
⇐ Columnar-Basalt Model: Unconfined Compression Test | Munson-Dawson Model: Pure Shear Test (FLAC3D) ⇒
| Was this helpful? ... | Itasca Software © 2024, Itasca | Updated: Dec 09, 2025 |
