Munson-Dawson Model: Biaxial Test (FLAC3D)

Note

The project file for this example may be viewed/run in FLAC3D.[1] The main data file used is shown at the end of this example.

This verification test for the Munson-Dawson model employs unequal biaxial compression loading, a stress state that triggers the Hosford criterion at a Lode angle distinct from those in biaxial or pure shear tests, due to the inequality of all three principal stress magnitudes (\(\sigma_{xx} \ne \sigma_{xx} \ne \sigma_{zz}\)).

The material properties are summarized in the table below.

shear

\(G\)

12.4 (GPa)

bulk

\(K\)

20.7 (GPa)

hosford

\(a\)

16

f-exponent

\(\chi\)

1

A-0

\(A_0\)

5.617e1 (\(s^{-1}\))

activation-ratio-0

\(Q_0/R\)

5123 (K)

n-0

\(n_0\)

1.595

A-1

\(A_1\)

8.386e22 (\(s^{-1}\))

activation-ratio-1

\(Q_1/R\)

12580.5 (K)

n-1

\(n_1\)

5.5

A-2

\(A_2\)

4.415e16 (\(s^{-1}\))

activation-ratio-2

\(Q_2/R\)

5123 (K)

n-2

\(n_2\)

6.279

B-1

\(B_1\)

6.086e6 (\(s^{-1}\))

B-2

\(B_2\)

3.034e-2 (\(s^{-1}\))

stress-limit

\(\sigma_0\)

20.57e6 (MPa)

stress-constant

\(q\)

5335

k-0

\(k_0\)

5.277e-2

c-0

\(c_0\)

8.882e-3 (\(K^{-1}\))

m-0

\(m_0\)

0.9201

k-1

\(k_1\)

3.052e12

c-1

\(c_1\)

8.882e-3 (\(K^{-1}\))

m-1

\(m_1\)

5.282

alpha-hardening

\(\alpha_h\)

3.367

beta-hardening

\(\beta_h\)

-0.6838

alpha-recovery

\(\alpha_h\)

0.58

beta-recovery

\(\beta_r\)

0.0

The test starts with zero stress. At t = 0 days, the stresses applied are \(\sigma_{xx} = 3.5\) MPa, \(\sigma_{yy} = 5\) MPa, and \(\sigma_{zz} = 0\) MPa. At t = 50 days, σ_xx is increased to 6 MPa, while the other stresses remain unchanged. This significant increase in σ_xx induces a step change in elastic strain, noticeable due to the minimal viscoplastic strains at these low levels of equivalent stress. Throughout the test as presented in Figure 1, the numerical results from FLAC3D and the reference analytical solutions in Reedlunn (2018) for the three total strains exhibit an exceptionally good match.

References

Reedlunn, B. Enhancements to the Munson-Dawson model for rock salt (No. SAND-2018-12601). Sandia National Laboratories, Albuquerque, NM, USA (2018).

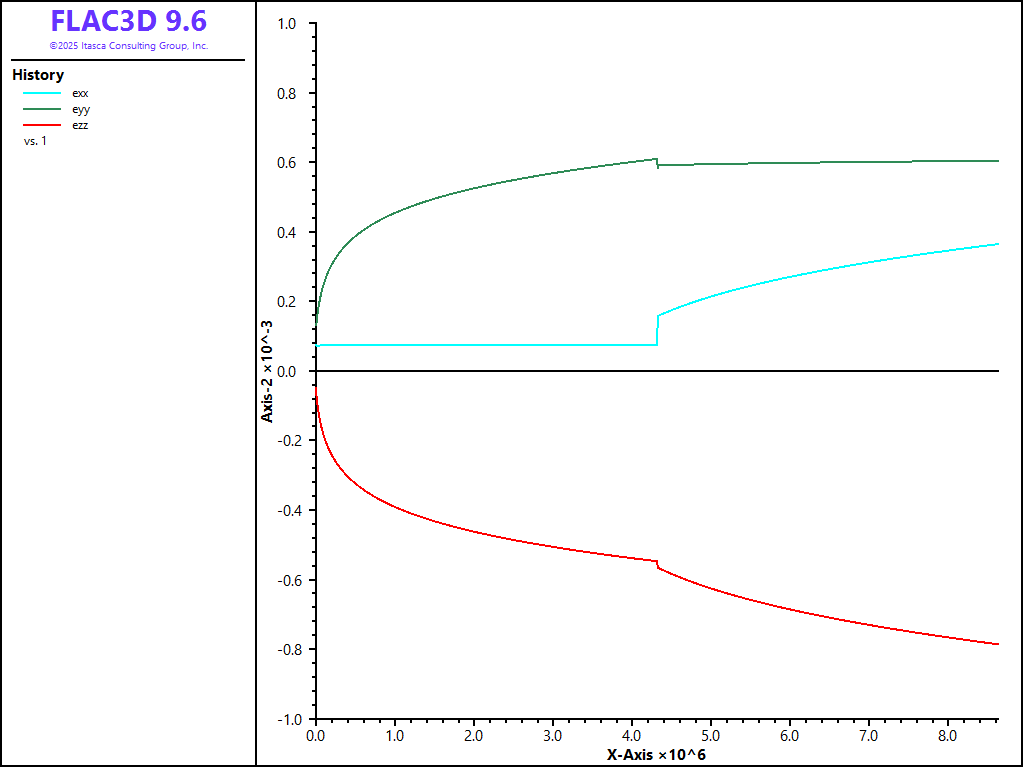
../../../../../_images/md-biaxial-strain.png

Figure 1: Biaxial test on a Munson-Dawson material: numerical strain values versus time.

Data File

model new
model large-strain off
fish automatic-create off
model title "Biaxial Compression test --- Munson-Dawson model"
model configure creep
model creep active off
;
zone create brick size 1 1 1
zone face skin
zone cmodel assign elastic
zone property density 2300 bulk 20.7e9 shear 12.4e9
;
zone initialize stress xx -0 yy 0 zz 0.0
model solve
;
model creep active on
zone cmodel assign munson-dawson
;; Cal-3B
zone property density 2300 temperature 300
zone property bulk 20.7e9 shear 12.4e9 f-exponent 1 hosford 16
zone property A-0 5.617e1  activation-ratio-0    5123 n-0 1.595
zone property A-1 8.386e22 activation-ratio-1 12580.5 n-1 5.5
zone property A-2 4.415e16 activation-ratio-2    5123 n-2 6.279
zone property B-1 6.086e6 B-2 3.034e-2 
zone property stress-limit 20.57e6 stress-constant 5335
zone property k-0 5.277e-2  c-0 8.882e-3 m-0 0.9201
zone property k-1 3.052e12  c-1 8.882e-3 m-1 5.282
zone property alpha-hardening 3.367 beta-hardening -0.6838
zone property alpha-recovery 0.58 beta-recovery 0.0
;
zone face apply stress-xx -3.5e6 range group 'East'
zone face apply stress-yy -5.0e6 range group 'North'
zone face apply velocity-z 0 range group 'Bottom'
zone face apply velocity-y 0 range group 'South'
zone face apply velocity-x 0 range group 'West'
;
[global zp = zone.head]
[global gp = gp.find(8)]
fish define sxx_
    global sxx_ = zone.stress.xx(zp)
    global syy_ = zone.stress.yy(zp)
    global szz_ = zone.stress.zz(zp)
    global exx_ = math.ln(1.0-gp.disp.x(gp))
    global eyy_ = math.ln(1.0-gp.disp.y(gp))
    global ezz_ = math.ln(1.0-gp.disp.z(gp))
end
model history creep time-total
fish history name 'sxx' sxx_
fish history name 'syy' syy_
fish history name 'szz' szz_
fish history name 'exx' exx_
fish history name 'eyy' eyy_
fish history name 'ezz' ezz_
history interval 20
; --- creep test ---
model creep timestep starting 1e-12
model creep timestep automatic
model creep timestep minimum 1e-12 
model creep timestep maximum 1000
model creep timestep upper-multiplier 0.99
model creep timestep lower-multiplier 1.01
;
model solve creep time-total [3600*24*50]
model save 'bi1'
;
model creep active off
zone face apply stress-xx -6.0e6 range group 'East'
zone face apply stress-yy -5.0e6 range group 'North'
model solve cycles 20
;
model creep active on
model creep timestep starting 1e-12
model creep timestep automatic
model creep timestep minimum 1e-12 
model creep timestep maximum 1000
model creep timestep upper-multiplier 0.99
model creep timestep lower-multiplier 1.01
;
model solve creep time-total [3600*24*100]
;history export '1' 'exx' 'eyy' 'ezz' file "biaxial-md.txt" truncate
model save 'biaxial-md'