Pseudostatic Analysis (FLAC2D)

Example Application

This example reproduces example 1.4.7 from the FLAC/Slope 8.1 manual. The project file for this example may be viewed/run in FLAC2D.[1] The main data file used is shown at the end of this example.

How To Read and Use Examples

Problem Statement

Pseudostatic analysis is a procedure commonly used to estimate the seismic stability of earth structures by representing the effects of an earthquake with constant horizontal and/or vertical accelerations. In limit equilibrium analysis, dimensionless horizontal and vertical pseudostatic acceleration coefficients, \(k_h\) and \(k_v\), are multiplied times the weight of the failure mass to calculate a safety factor. The coefficients are defined as \(k_h = a_h/g\) and \(k_v = a_v/g\), where \(a_h\) and \(a_v\) are the horizontal and vertical pseudostatic accelerations, and \(g\) is the static gravitational magnitude. The magnitude of the coefficients is related to the severity of the earthquake. Kramer (1996) provides further information on the pseudostatic approach and a discussion on the selection of pseudostatic coefficients.

A pseudostatic analysis can be conducted with FLAC2D by adjusting the gravitational vector to include the pseudostatic acceleration. This procedure is demonstrated by comparing FLAC2D to a pseudostatic limit equilibrium analysis presented by Kramer (1996). A simple 30 ft high 2:1 (H:V) slope is subjected to an earthquake that is represented by \(k_h = 0.1\) and \(k_v = 0.0\). The slope consists of two soil layers overlaying a rigid bedrock. Soil 1 is a 30 ft thick layer immediately above the bedrock, and Soil 2 is a 20 ft thick layer above Soil 1. The factor of safety reported by Kramer for the pseudostatic analysis of this slope with \(k_h = 0.1\) and \(k_v = 0.0\) is 1.28, assuming a circular failure surface. Kramer also reports that the factor of safety for a static limit equilibrium analysis of the slope is 1.79.

Model Construction

The model is built using the Slope Wizard in Sketch. The following parameters are entered:

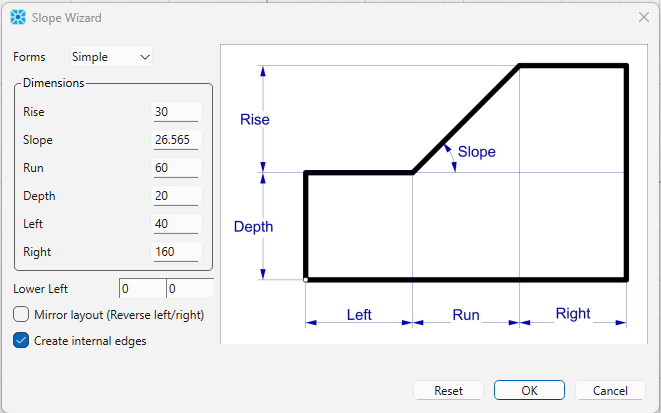
Note that you do not need to enter the slope angle; it is automatically calculated from the rise and run. A horizontal line is then drawn at y=30 to separate the soil layers.

Next use autosize () on the “Mesh Tools” pulldown to set zone length to 3. Then use mesh all polygons (), also on the “Mesh Tools” pulldown, to add zones to the model blocks. The model should appear as shown:

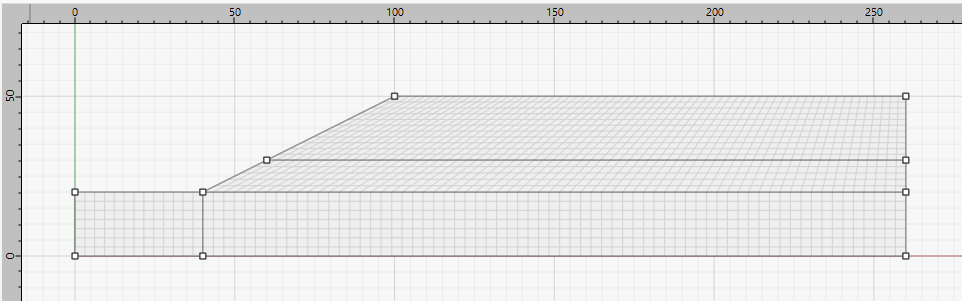
Click on the top block and set its group name to “soil2”. Then assign group name “soil1” to the bottom 3 blocks. Finally, press the create zones button () to create the zones. Save the project and the model state.

After the zones are created, make a new plot and add Zones. In the attributes, change the group slot to Construction to see the model as shown in Figure 3.

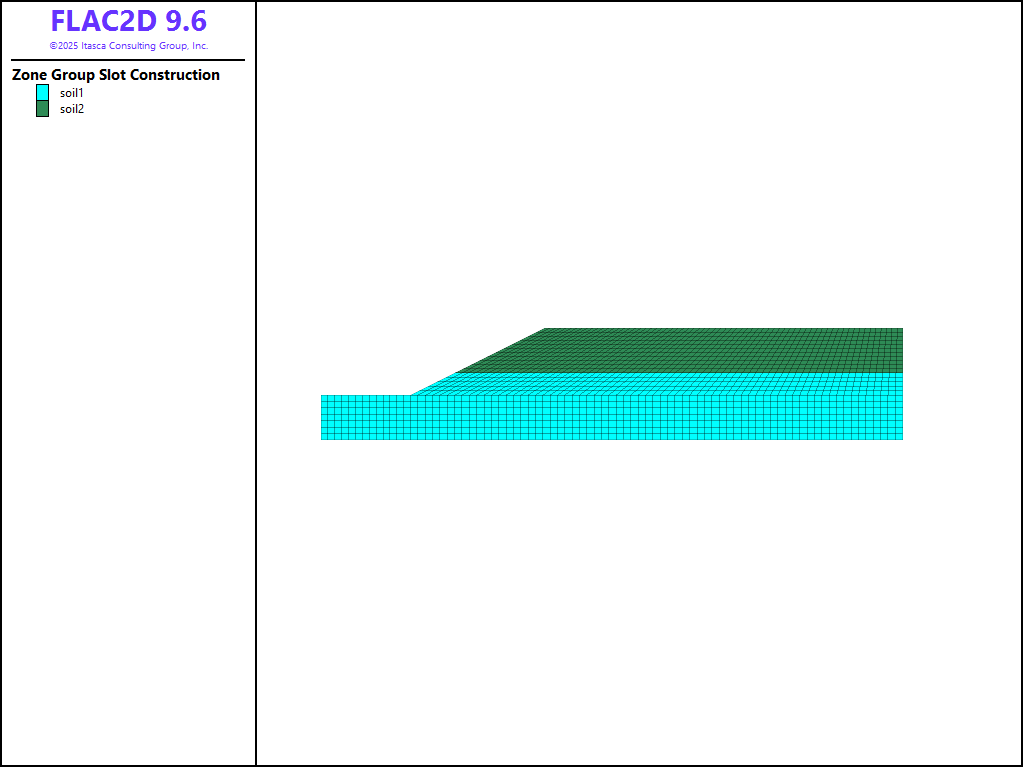
Figure 3: Model used in pseudostatic analysis of a simple slope.

After building the model, create a data file and add commands as shown in static.dat. The properties of Soil 1 are:

• unit weight: 125 lb/ft³

• cohesion (c): 1000 lb/ft²

• friction angle: (φ) 0.0

The properties of Soil 2 are:

• unit weight: 110 lb/ft³

• cohesion (c): 600 lb/ft²

• friction angle: (φ) 0.0

Note that for this analysis the tensile strengths of the soils are set to a high value to prevent tensile failure, for comparison to the limit equilibrium solution.

After solving to initial equilibrium, the gravitational vector is adjusted to include the pseudostatic acceleration by the following command:

model gravity (-3.22,-32.2)

A factor of safety analysis is then performed.

Results

The factor of safety calculated from the pseudostatic FLAC2D run is 1.25. A circular failure mode is indicated in Figure 4. The results compare well with the pseudostatic limit equilibrium solution. The static factor-of-safety is also calculated to be 1.69, and the failure surface result is shown in Figure 5.

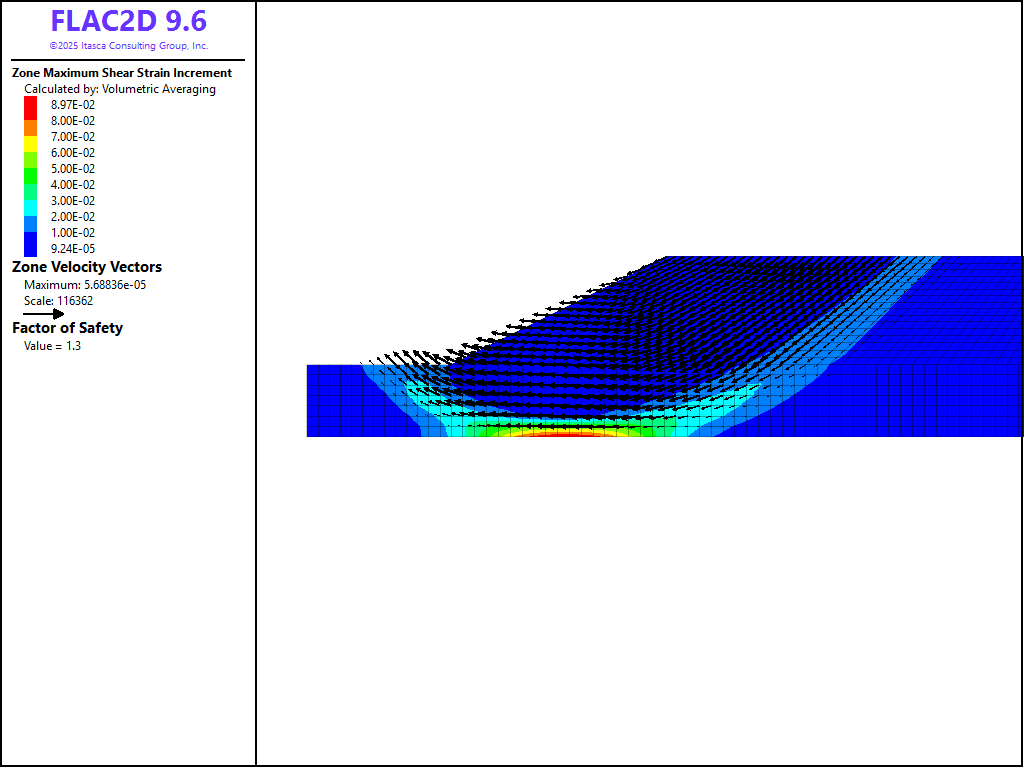
Figure 4: Factor-of-safety results for pseudostatic analysis of a simple slope.

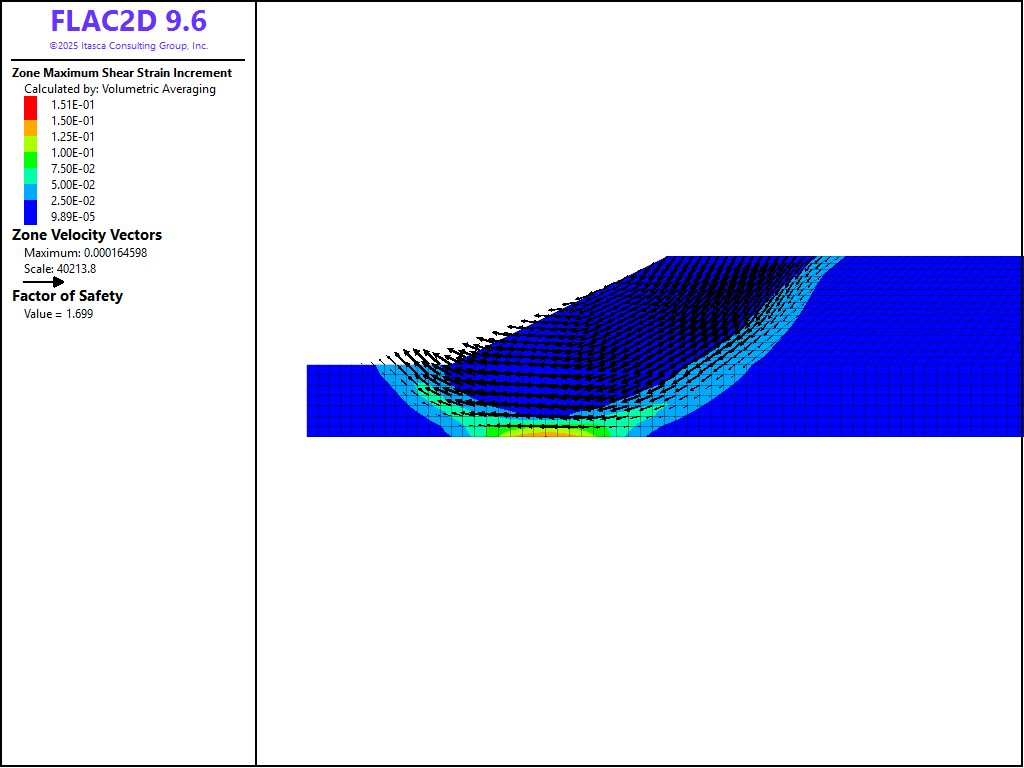
Figure 5: Factor-of-safety results for static analysis of a simple slope.

References

Kramer, S. L. Geotechnical Earthquake Engineering. New Jersey: Prentice-Hall (1996).

Data Files

static.dat

model restore 'mesh'

model gravity 32.18504
model large-strain off

zone cmodel assign mohr-coulomb
zone property density 3.882 bulk 2.1E6 shear 6.3E5 ... 
              cohesion 1000.0 friction 0.0 dilation 0.0 tension 1.0E10 ...
              range group 'soil1'
zone property density=3.416 bulk=2.088543E6 shear=6.2656E5 cohesion=600.0 ...
              friction=0.0 dilation=0.0 tension=1.0E10 range group 'soil2'
              
zone face skin
zone face apply velocity-x 0 range group 'East' or 'West'
zone face apply velocity (0,0) range group 'Bottom'

model factor-of-safety filename 'static'

pseudostatic.dat

model restore 'mesh'

; note horizontal gravity!
model gravity (-3.22,-32.2)

model large-strain off

zone cmodel assign mohr-coulomb
zone property density 3.882 bulk 2.1E6 shear 6.3E5 ... 
              cohesion 1000.0 friction 0.0 dilation 0.0 tension 1.0E10 ...
              range group 'soil1'
zone property density=3.416 bulk=2.088543E6 shear=6.2656E5 cohesion=600.0 ...
              friction=0.0 dilation=0.0 tension=1.0E10 range group 'soil2'

zone face skin
zone face apply velocity-x 0 range group 'East' or 'West'
zone face apply velocity (0,0) range group 'Bottom'

model factor-of-safety filename 'pseudostatic'

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).