Maxwell/Kelvin/Burgers Model: Parallel-Plate Viscometer (FLAC2D)

Model Verification

The project file for this example may be viewed/run in 3DEC.[1] The main data file used is shown at the end of this example.

How To Read and Use Examples

This example verifies the classical Maxwell model and Burgers model. Suppose that a material with viscosity \(\eta\) is steadily squeezed between two parallel plates that are moving at a constant velocity \(V_0\). The two plates have length 2 \(l\) and are a distance 2 \(h\) apart. The material is prevented from slipping at the plates. The approximate analytical solution, given by Jaeger (1969), is

\[\begin{split}\begin{split} V_x\ &=\ {{3 V_o x\ (h^2 - y^2)} \over {2 h^3}} \\ V_y\ &=\ {{V_o y (y^2 - 3 h^2)} \over {2 h^3}} \\ \sigma_{xx}\ &=\ 3 \eta V_o\ \biggl[ {{3 (h^2 - y^2) + x^2 - l^2} \over {2 h^3}} \biggr] \\ \sigma_{yy}\ &=\ 3 \eta V_o\ \biggl[ {{y^2 - h^2 + x^2 - l^2} \over {2 h^3}} \biggr] \\ \sigma_{xy}\ &=\ -3 \biggl[ {{ V_o\ \eta\ x\ y} \over {h^3}} \biggr] \end{split}\end{split}\]

The problem is illustrated in Figure 1.

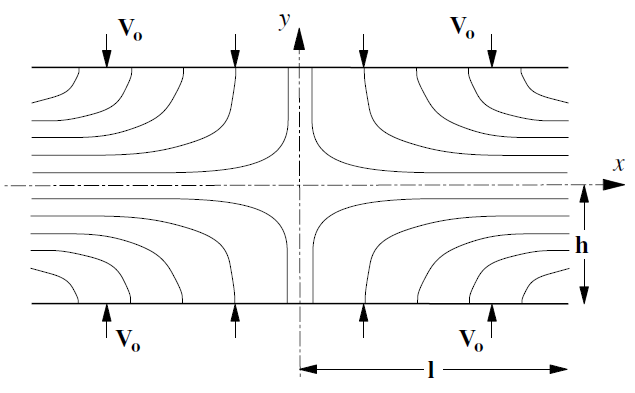
Figure 1: Parallel-plate viscometer showing velocity streamlines (Jaeger 1969).

To solve the problem with FLAC2D, advantage can be taken of the symmetry about the \(x\)- and \(y\)-axes. Only the top-right quadrant needs to be modeled. For compatibility with the approximations of the analytical solution, artificial forces have to be applied at the “free” right-hand edge, and small-strain logic is used.

The material properties are

shear modulus	5 × 108 Pa
bulk modulus	1.5 × 109 Pa
viscosity	1 × 1010 kg/ms

The Maxwell model component is also tested in the Burgers-Mohr model (zone cmodel burgers-mohr) for the viscometer test. The values of cohesion and tensile strength are set high to prevent plastic failure in the viscoplastic model so it is equivalent to the classical Burgers model. The additional commands for this model are contained in main data files. Upon execution of the data file with each model activated, results identical to those produced with the classical viscoelastic model are obtained.

The FLAC2D grid is shown in Figure 2.

The analytical solution is calculated with FISH function analytical, using the extended arrays to store the calculated values. A good agreement was obtained between FLAC2D and the closed-form solution. The contours of \(x\)-velocity are plotted in Figure 3. The corresponding analytical solution is shown in Figure 4. The \(\sigma_{xx}\)-contours are shown in Figure 5, and the analytical values in Figure 6.

Figure 2: FLAC2D grid for parallel-plate test.

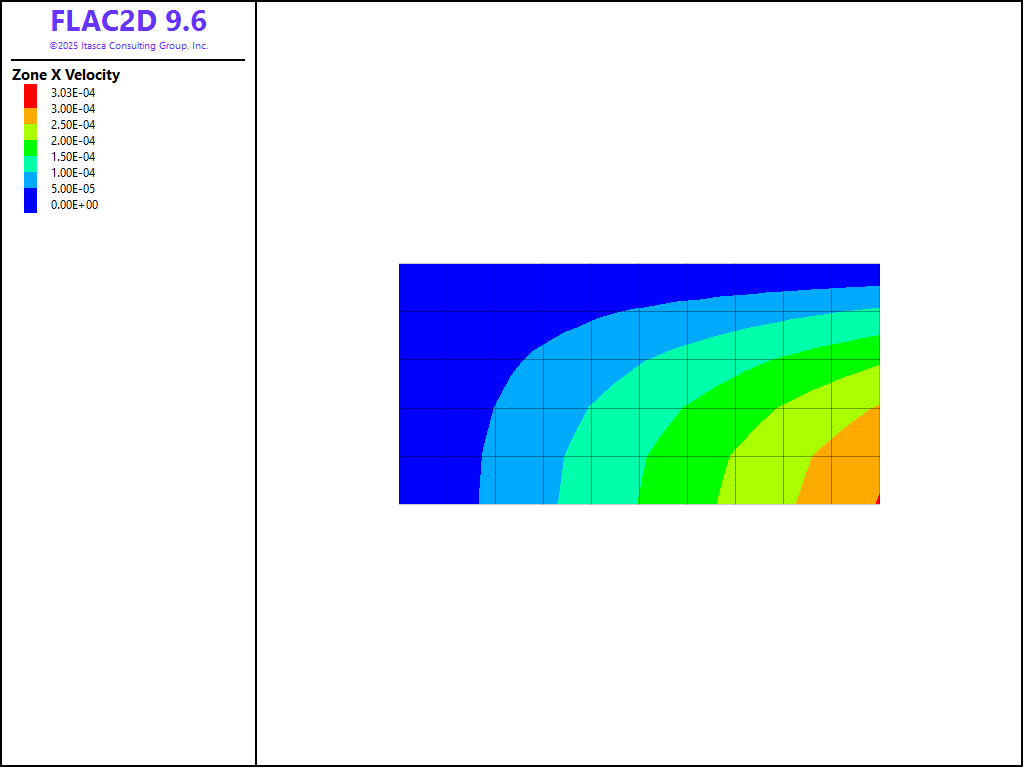
Figure 3: Contours of \(x\)-velocity from FLAC2D.

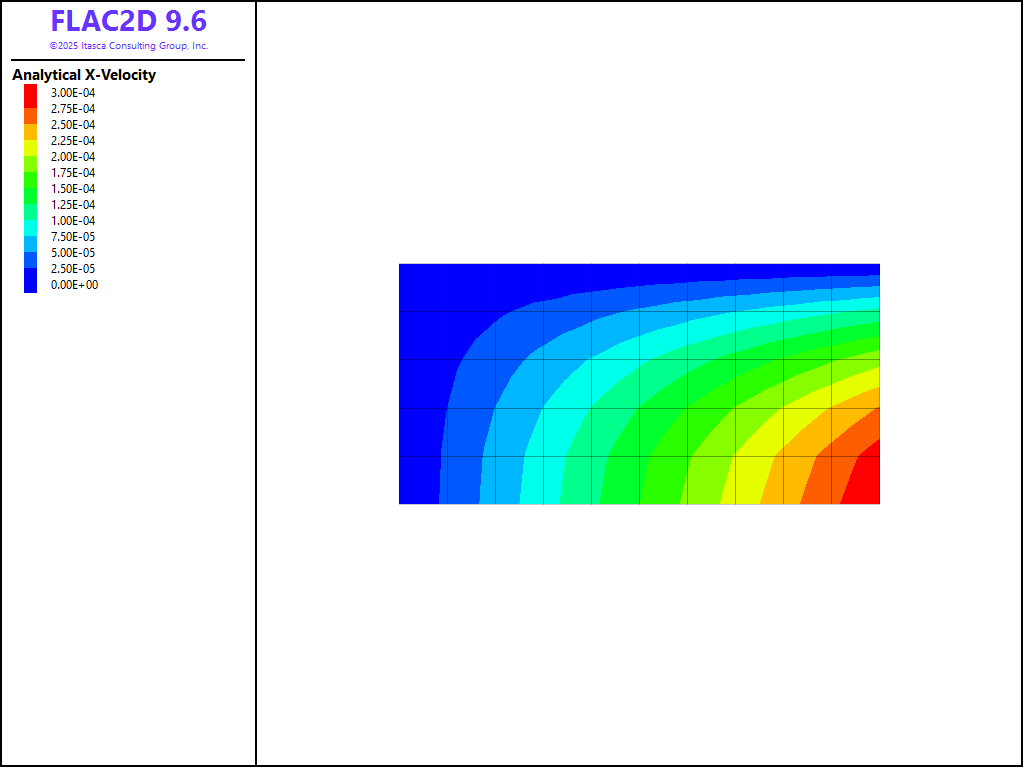
Figure 4: Contours of \(x\)-velocity from the analytical solution (from gridpoint extra array 1).

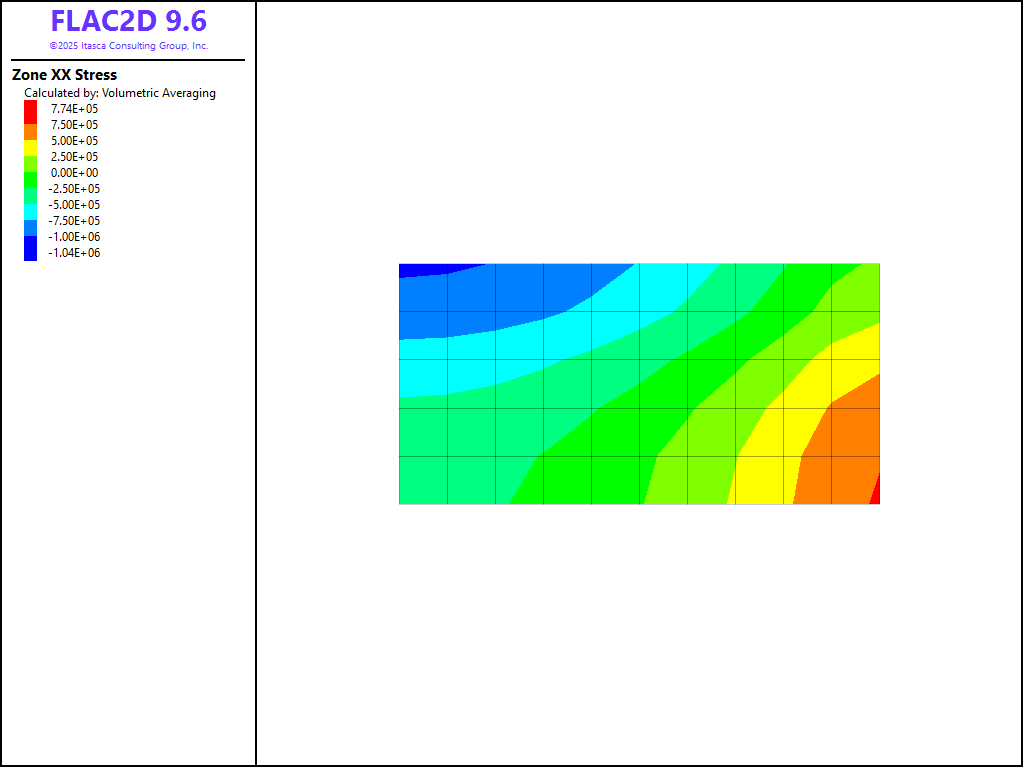
Figure 5: Contours of \(\sigma_{xx}\) from FLAC2D.

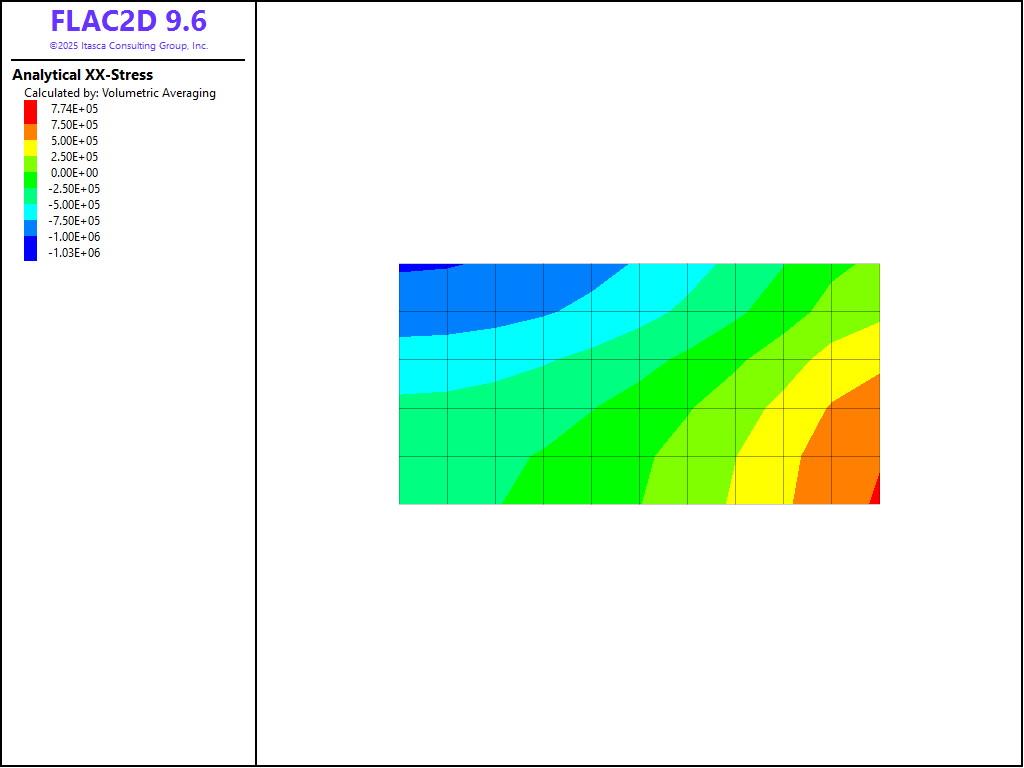
Figure 6: Contours of \(\sigma_{xx}\) from the analytical solution (from zone extra array 1).

Data File

;------------------------------------------------------------
; Parallel plate viscometer -- classical model
;-------------------------------------------------------------------
model new
model large-strain off
fish automatic-create off
model title "PARALLEL-PLATE VISCOMETER (CLASSICAL VISCOSITY)"
model configure creep
;
program call 'AnalyticalSolution'
;
zone create quadrilateral size 10 5
zone face skin
zone cmodel assign maxwell
zone property shear 0.5e9 bulk 1.5e9 viscosity 1e10
;
zone face apply velocity-x     0 range group 'Top'
zone face apply velocity-y -1e-4 range group 'Top'
zone face apply velocity-x   0.0 range group 'West'
zone face apply velocity-y   0.0 range group 'Bottom'

; forces at r.h.s boundary
zone gridpoint fix force-applied-x 4.50e5  range position-x 10 position-y 0
zone gridpoint fix force-applied-x 8.64e5  range position-x 10 position-y 1
zone gridpoint fix force-applied-x 7.56e5  range position-x 10 position-y 2
zone gridpoint fix force-applied-x 5.76e5  range position-x 10 position-y 3
zone gridpoint fix force-applied-x 3.24e5  range position-x 10 position-y 4
;
zone gridpoint fix force-applied-y -2.4e5  range position-x 10 position-y 1
zone gridpoint fix force-applied-y -4.8e5  range position-x 10 position-y 2
zone gridpoint fix force-applied-y -7.2e5  range position-x 10 position-y 3
zone gridpoint fix force-applied-y -9.6e5  range position-x 10 position-y 4
;
model creep active on
model creep timestep fix 1
model save 'ini'
;
model step 900
[analytical(-1e-4,5,10,1e10)]
model save 'viscplate-maxwell'
;
model restore 'ini'
zone cmodel burgers-mohr
zone property shear-maxwell 0.5e9 bulk 1.5e9 viscosity-maxwell 1e10 ...
              cohesion 1e10 tension 1e10 ;  model cvisc
model step 900
[analytical(-1e-4,5,10,1e10)]
model save 'viscplate-burgers-mohr'
;
program return

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).