Hollow Sphere Subject to an Internal Blast (FLAC2D)
The project file for this example may be viewed/run in FLAC2D.[1] The main data file used is shown at the end of this example.
This problem concerns the propagation of a spherical wave due to an impulsive pressure (explosion) in a sphere. In unbounded (i.e., infinite) media, two types of waves can exist: compression and shear waves. In this problem, the axisymmetric nature of the problem eliminates the shear wave. Therefore, only the solution for the compression wave need be sought. The problem provides a test of the dynamic capabilities of FLAC2D and is applicable to impact and explosion modeling.
The analytical solution for this problem, assuming that the material is elastic and isotropic, was derived by Blake (1952). The solution is based on the following governing equation:
where: |
\(C_p\) |
= compressional wave velocity; |
\(t\) |
= time; |
|
\(\phi\) |
= a potential function; and |
|
\(\bigtriangledown^2\) |
= Laplacian operator. |
Let \(p(t)\) be an impulse that jumps from zero to \(p_0\) at \(t\) = 0, and then decays exponentially with the time constant \(\alpha^{-1}\). Thus, the pressure function can be defined by
A step function of the pressure (\(\alpha\) = 0) will be used for this problem. For such a pressure function, the potential function that satisfies the governing equation is
where: |
\(a\) |
= radius of the sphere; |
\(K\) |
= \({{1 - \nu} \over {2 (1 - 2 \nu)}}\); |
|
\(\nu\) |
= Poisson’s ratio; |
|
\(r\) |
= radial coordinate; |
|
\(\alpha_0\) |
= \({{C_p} \over {2 a K}}\) = radiation damping constant; |
|
\(\tau\) |
= \(t - {{ r - a} \over {C_p}}\); and |
|
\(\omega_0\) |
= \({{c} \over {2 a K}}\ \sqrt{4 K - 1}\) = natural frequency. |
The radial displacement can be found by differentiating the potential function with respect to radial distance.
A sphere embedded in an infinite, isotropic medium is simulated in two ways. Figures 1 and 2 show two different grids used for the simulation. The first grid is an axisymmetric representation in which the outer boundary is circular. The second grid has a rectangular outer boundary. The radius of the inner boundary is assumed to be 10 m, and the outer boundary is located at a distance approximately ten times that of the inner boundary.
For both grids, normal movement is prevented at the axes of symmetry, and a viscous condition is imposed on the outer boundary to absorb the wave. The material properties used for the problem are
shear modulus (\(G\)) |
1 × 1010 |
bulk modulus (\(K\)) |
1.665 × 1010 Pa |
density (\(\rho\)) |
1675 kg/m3 |
A pressure equal to 1000 Pa is applied at the inner boundary to simulate the blasting.
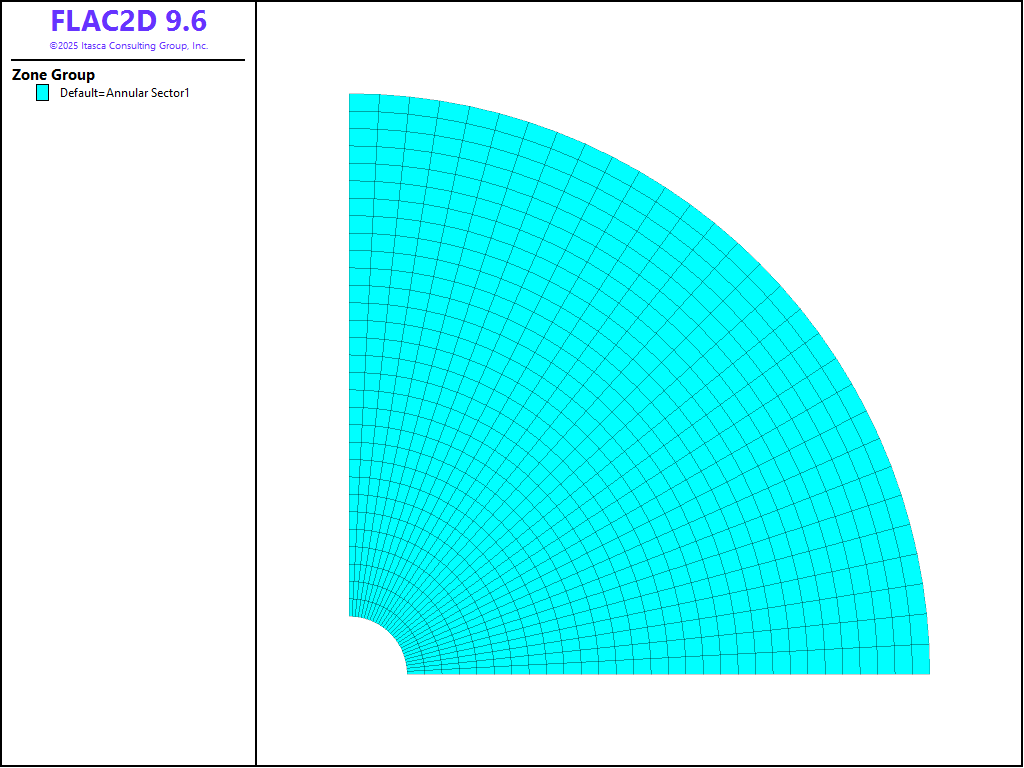
Figure 1: Circular axisymmetric grid.
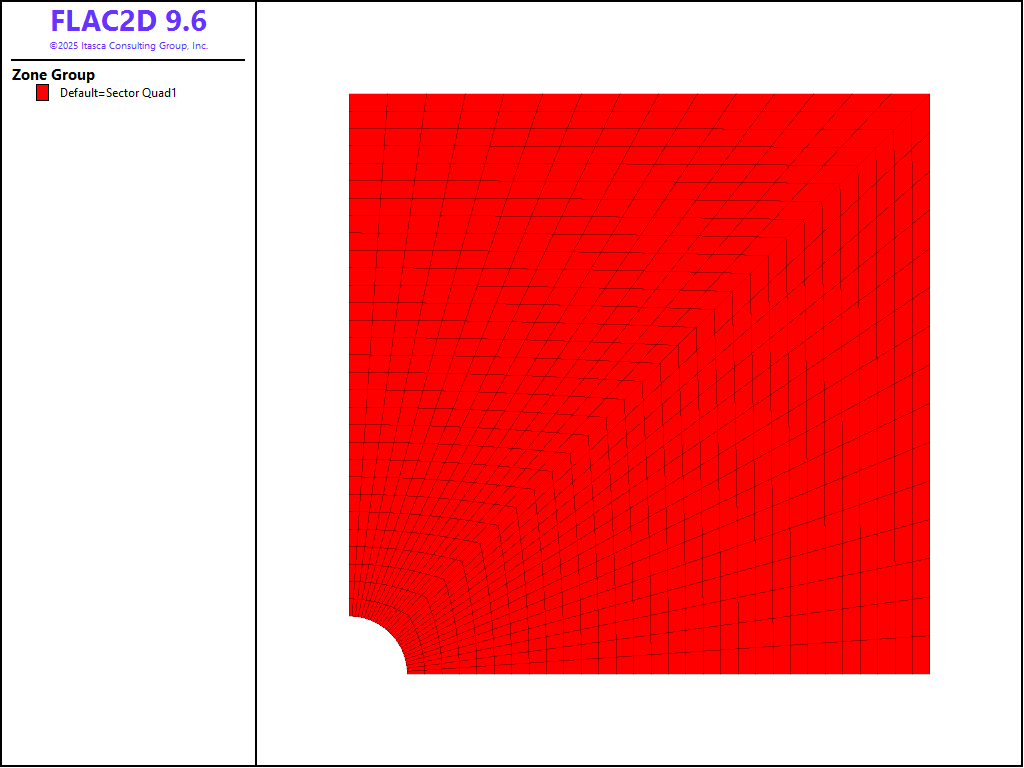
Figure 2: Rectangular axisymmetric grid.
The radial displacement histories recorded up to 0.1 second at \(r\) = 2.05\(a\), 3.42\(a\), and 4.87\(a\) are given in Figures 3 and 4 for the circular and rectangular simulation, respectively. The delay of the response at locations far from the sphere can be noted in both cases. In both cases, FLAC2D is able to capture the response at peak and steady states. The fluctuation at late time is due to the fact that the radiated wave is not absorbed completely by the viscous boundary.
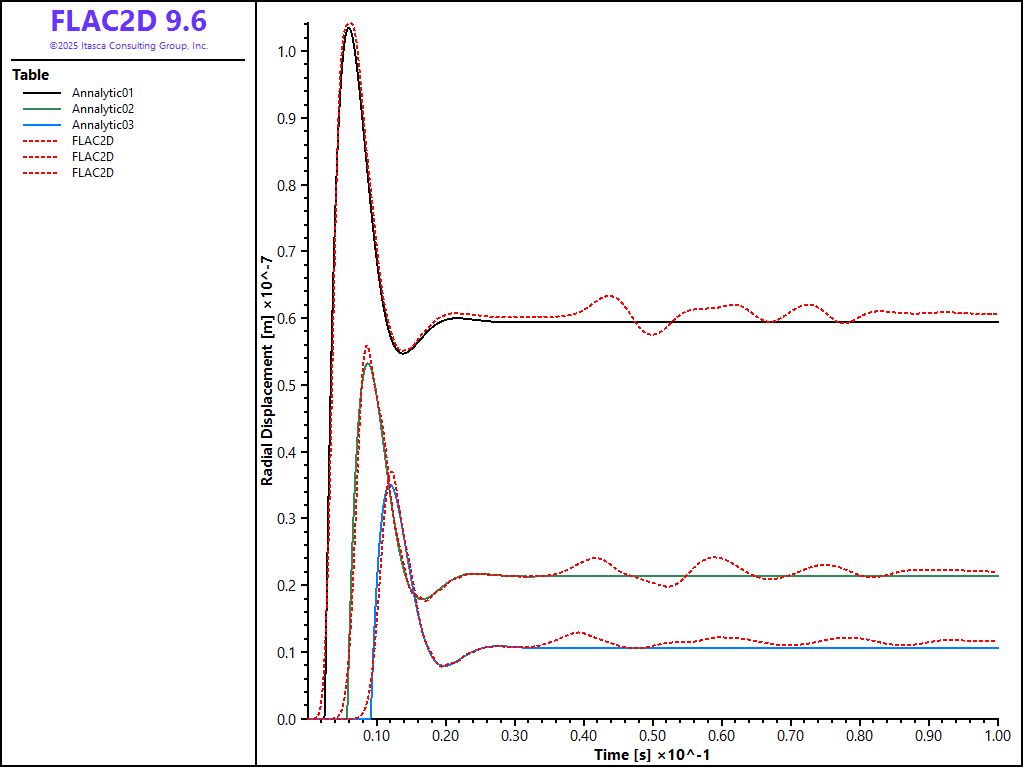
Figure 3: Radial displacement histories at r = 2.05a, 3.42a, and 4.87a (circular case).
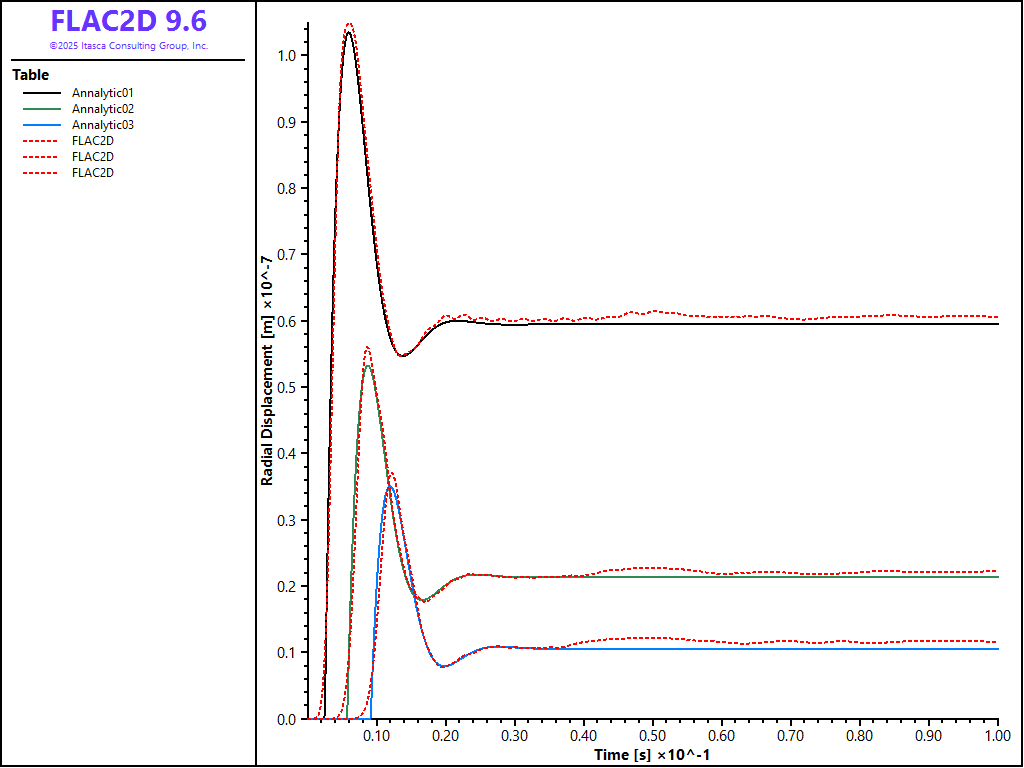
Figure 4: Radial displacement histories at r = 2.05a, 3.42a, and 4.87a (rectangular case).
References
Blake, F. G. “Spherical Wave Propagation in Solid Media,” J. Acous. Soc. Am., 24(2), 211-215 (1952).
Data Files
SphericalPulse1D.dat
SphericalPulse.dat
Endnote
| Was this helpful? ... | Itasca Software © 2026, Itasca | Updated: Feb 07, 2026 |
