Comparison of Three Damping Cases

Verification Problem

The project file for this example may be viewed/run in FLAC3D.[1] The main data file used is shown at the end of this example.

How To Read and Use Examples

The i Integration of Damping Schemes and Nonlinear Material Models for Geo-materials section in i Dynamic Damping presents three damping schemes:

• Natural Damping with the Mohr-Coulomb Model

• Hysteretic Damping with the Linear Elastic Model

• Hysteretic Damping with the Mohr-Coulomb Model

The energy dissipation for these three damping cases is compared by exercising the equations for \(G/G_{max}\) and \(D\) over a cyclic strain range. A FISH function, damp, listed below, performs this exercise over a cyclic shear strain, \(\gamma_c\), from 0.0001 to 4.0. The value for \(\gamma_m\) is set to 0.01 and the value for \(\gamma_{ref}\) is set to 0.02. The results for \(G/G_{max}\) versus log \(\gamma_c/\gamma_m\), based upon Equations (71), (77), (90), and (91), are plotted in Figures 1. The results for \(D\) versus log \(\gamma_c/\gamma_m\), based upon Equations (76), (85), and (97), are plotted in Figure 2.

The inclusion of hysteretic damping is shown to reduce the shear modulus from the initial value of \(G_{max}\), and increase the damping ratio (compared to the elastic-only response). The damping ratio increases monotonically with shear strain amplitude and approaches the asymptotic value of \(2 / \pi\) for all three cases.

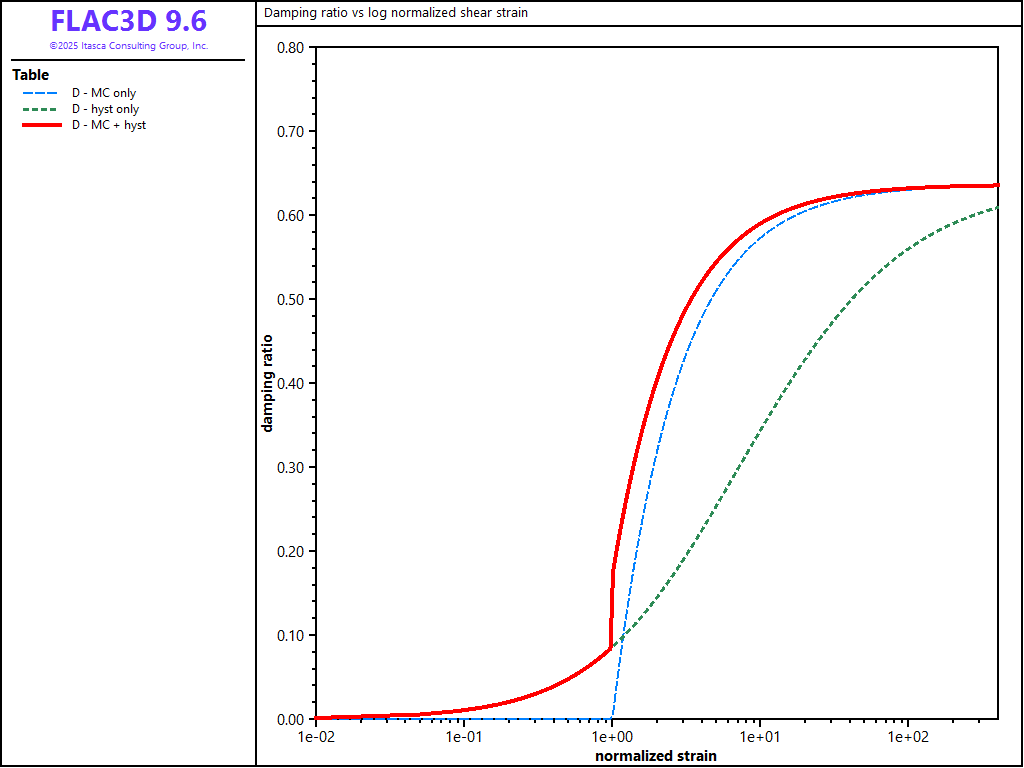
Figure 1: Normalized shear modulus vs. log normalized shear strain for three damping cases in FLAC3D.

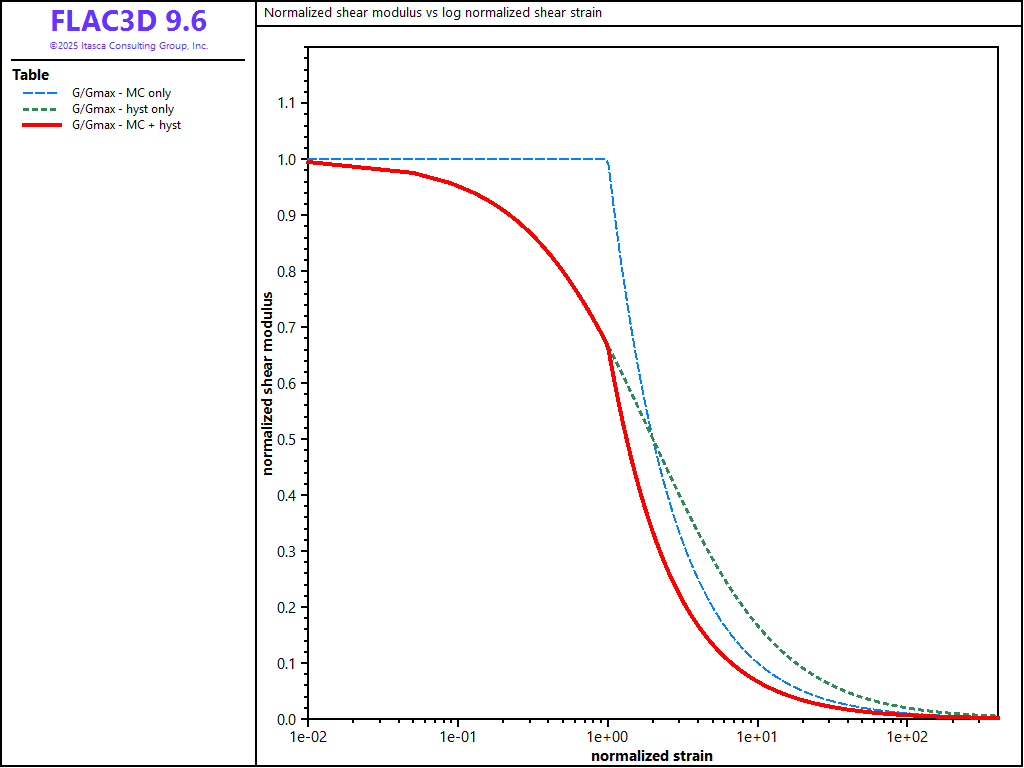
Figure 2: Damping ratio vs. log normalized shear strain for three damping cases in FLAC3D.

Figure 3: Normalized shear modulus vs. log normalized shear strain for three damping cases in FLAC2D.

Figure 4: Damping ratio vs. log normalized shear strain for three damping cases in FLAC2D.

Data File (FLAC3D)

Damping-Compare.dat

;---------------------------------------------------------------------
;              Compare damping
;              Driver file
;---------------------------------------------------------------------
model new
fish automatic-create off
; assume Gmax = 1.
fish define damp
    ; strain range
    local r1   = 0.0001 ; min
    local r2   = 4.     ; max
    local rm   = 0.01
    local rref = 0.02
    local np   = 10000
    local rinc = (r2-r1)/float(np)
    local r = r1
    loop local n (1,np)
        local rrat = r / rm
        if r <= 0. then
            local ghyst = 1.
            local dhyst = 0.
        else
            local tau   = r/(1.+r/rref)
            ghyst = tau/r
            local rf    = r/rref
            local rf2   = rf*rf
            local rln   = rf - math.ln(1.+rf)
            dhyst = 2./math.pi*(2.*(1.+rf)/rf^2*rln-1.)
        endif
        if r < rm then
            local gmohr = 1.
            local dmohr = 0.
        else
            gmohr = rm/r
            dmohr = 2.*(r-rm)/(math.pi*r)
        endif
        if r <= rm then
            local gcomb = 1./(1.+r/rref)
        else
            gcomb = 1./((1.+rm/rref)*r/rm)
        endif
        if r <= rm then
            local dcomb = dhyst
        else
            rf    = rm/rref
            rf2   = rf*rf
            rln   = rf - math.ln(1.+rf)
            dcomb = 2./math.pi*(2.*(1.+rf)/rf^2*rln-1.)*rref/r
            dcomb = dcomb + 2./math.pi*(r-rm)/r
        endif
        rrat = rrat
        table(11,rrat) = gmohr
        table(21,rrat) = dmohr
        table(12,rrat) = ghyst
        table(22,rrat) = dhyst
        table(13,rrat) = gcomb
        table(23,rrat) = dcomb
        r = r + rinc
    endloop
end
[damp]

Data File (FLAC2D)

Damping-Compare.dat

;---------------------------------------------------------------------
;              Compare damping
;              Driver file
;---------------------------------------------------------------------
model new
fish automatic-create off
;
; assume Gmax = 1.
;
fish define damp
    ; strain range
    local r1   = 0.0001 ; min
    local r2   = 4.     ; max
    local rm   = 0.01
    local rref = 0.02
    local np   = 10000
    local rinc = (r2-r1)/float(np)
    local r = r1
    loop local n (1,np)
        local rrat = r / rm
        if r <= 0. then
            local ghyst = 1.
            local dhyst = 0.
        else
            local tau   = r/(1.+r/rref)
            ghyst = tau/r
            local rf    = r/rref
            local rf2   = rf*rf
            local rln    =rf - math.ln(1.+rf)
            dhyst = 2./math.pi*(2.*(1.+rf)/rf^2*rln-1.)
        endif
        if r < rm then
            local gmohr = 1.
            local dmohr = 0.
        else
            gmohr = rm/r
            dmohr = 2.*(r-rm)/(math.pi*r)
        endif
        if r <= rm then
            local gcomb = 1./(1.+r/rref)
        else
            gcomb = 1./((1.+rm/rref)*r/rm)
        endif
        if r <= rm then
            local dcomb = dhyst
        else
            rf    = rm/rref
            rf2   = rf*rf
            rln   = rf - math.ln(1.+rf)
            dcomb = 2./math.pi*(2.*(1.+rf)/rf^2*rln-1.)*rref/r
            dcomb = dcomb + 2./math.pi*(r-rm)/r
        endif
        rrat = math.log(rrat)
        table(11,rrat) = gmohr
        table(21,rrat) = dmohr
        table(12,rrat) = ghyst
        table(22,rrat) = dhyst
        table(13,rrat) = gcomb
        table(23,rrat) = dcomb
        r = r + rinc
    endloop
end
[damp]
program return

Endnote

[1]

This example is listed under the present document title in the i Examples dialog (use the menu command Help -> Examples… to access).